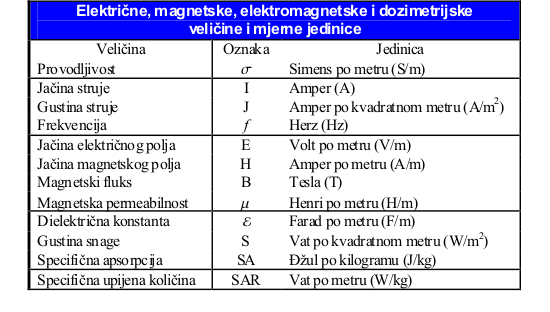
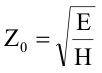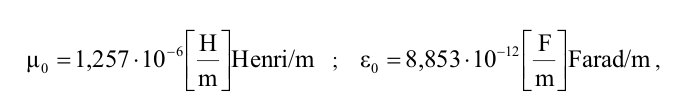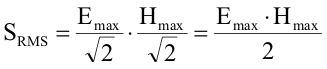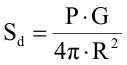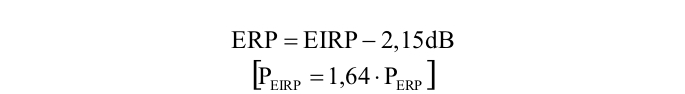Kod razmatranja prostiranja i zračenja elektromagnetskih talasa potrebno je poznavati njihove osnovne električne karakteristike kako bi se dobila što realnija procjena uticaja elektromagnetskog zračenja na čovječiji organizam. U tabeli 1.1 predstavljene su osnovne mjerne jedinice koje se koriste kod razmatranja električnih karakteristika EM talasa.

1.3.1.  Karakteristična impedansa slobodnog prostora (top)

Karakteristična impedansa prostora podrazumijeva odnos transvezalnih komponenti električnog i magnetskog polja. U našem slučaju polazimo od pretpostavke da se radi o ”dalekoj zoni” gdje su vektori električnog i magnetskog polja međusobno normalni.
Veličina gustine energije u talasu može se izračunati iz vektorskog  proizvoda.

Za ugao od 90⁰, kao što je slučaj u dalekoj zoni (sin 90⁰ = 1)

Kada pogledamo naš elektromagnetski talas u slobodnom prostoru (vidi sliku 1.11), gdje je količnik električnog i magnetskog polja jednak impedansi u slobodnom prostoru, možemo reći da je:

je impedansa i jednaka je količniku E i H, i ne zavisi od veličina tih polja [10]. Slobodni prostor pruža otpor elektromagnetskom zračenju. On ima permeabilnost (odnos gustine magnetskog fluksa koji nastane u nekoj sredini i jačine magnetskog polja koje ga je proizvelo) i dielektričnu konstantu – propustljivost (odnos gustine električnog fluksa koji nastane u nekoj sredini i jačine električnog polja koje ga je proizvelo).  Za slobodan prostor ove dvije veličine imaju vrijednost:

pa  se primjenom Maksvelovih jednačina dobija:

1.3.2.  Gustina snage elektromagnetskog talasa (top)

Elektromagnetski talasi prenose elektromagnetsku energiju čija sekoličina karakteriše gustinoms nage (S) ili Pointingovimvektorom [1].
Pointingov vektor ili gustina snage EM polja jeste količina energije koja prođe kroz površinu od 1 m², normalnu na pravac prostiranja talasa.
Gustina snage EM talasa predstavlja veoma značajnu veličinu koja karakteriše snagu elektromagnetskog talasa i direktni je pokazatelj izloženosti zračenju EM talasa.

Električno (E) polje se obično izražava u voltima po metru (V/m). Slično tome, magnetsko (H) polje se određuje u A/m. Proizvod ove dvije vrijednosti je gustina energije (napon puta struja jednako je snazi, po Omovom zakonu).
Rezultujuće jedinice su vati po metru kvadratnom (W/m²), ili češće mili-vati po centimetru kvadratnom (mW/cm²).

Veličina gustine snage EM talasa (S) određuje se izrazom:

S [W/m²] = E [W/m] × H [W/m]

Veličina intenziteta električnog (E) i magnetskog (H) polja elektromagnetskog talasa u slobodnom prostoru međusobno su vezane izrazom:

E [V/m] = 377ohm × H [A/m],

gdje je: 377ohm – karakteristična impedansa slobodnog prostora.

Prema tome, veličina Pointingovog vektora ili gustine snage elektromagnetskog talasa (S) je:

S [W/m²] = 377ohm × H² [A/m],

 izražena preko intenziteta magnetskog polja, ili

S [W/m²] = = 0.00265 × E² [V/m],

izražena preko intenziteta električnog polja.

Smjer Pointingovog vektora ili vektora gustine snage EM talasa (S) određuje se pravilom tri prsta desne ruke.

Ovo pravilo se formuliše ovako: ako se palac, kažiprst i srednji prst desne ruke postave međusobno normalno, s tim da se palac postavi u smjeru vektora E, a kažiprst u smjeru vektora H, onda srednji prst pokazuje smjer vektora (S).

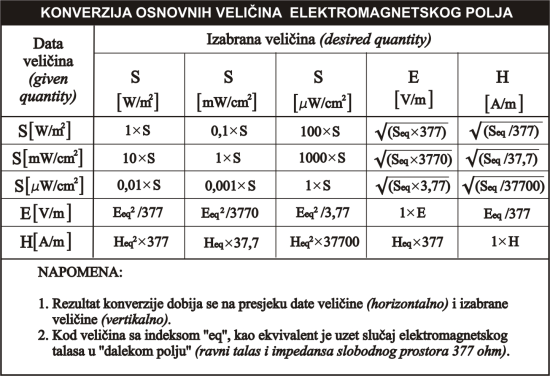
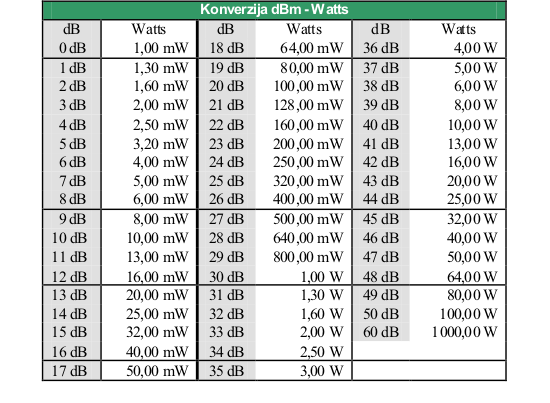
Radi lakšeg izračunavanja, u tabeli 1.2 date su osnovne jedinice i obrazci za izračunavanje karakterističnih vrijednosti elektromagnetskog polja, sa mogućnošću konverzije.

Tabela se može primjenjivati samo u slučaju ”daleke zone” elektromagnetskog polja gdje su vektori električnog i magnetskog polja međusobno normalni. U tom slučaju impedansa slobodnog prostora  ima vrijednost od  377 oma.

1.3.3.  Srednja vrijednost gustine EM polja (RMS) (top)

Gustina energije elektromagnetnog talasa je u vezi sa električnim i magnetskim poljima   na taj  način što je ona njihov proizvod.
S obzirom da su elektromagnetski talasi sinusnog oblika, često se za gustinu energije  koristi njena srednja vrijednost RMS (Root Mean Square). Ova vrijednost se dobija kada se veličine maksimalnih amplituda električnog i magnetskog polja podijele sa kvadratnim korijenom iz 2. S obzirom da je:

kada primjenimo uslov za izračunavanje RMS vrijednosti gustine EM polja, dobijamo:

1.3.4.  Snaga EM talasa u zavisnosti od rastojanja

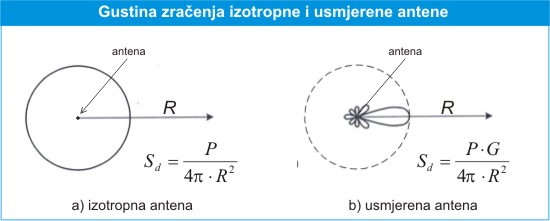
Ako neki izvor zrači energiju podjednako u svim pravcima (izotropna antena), gustina snage elektromagnetskog polja (S_d) na udaljenosti (R) od izotropne antene biće količnik snage predajnika (P)  i površine sfere (D_s) koja okružuje izotropnu antenu, što je predstavljeno formulom:

Ova  relacija iskazuje činjenicu da je ukupna snaga zračenja jednako raspoređena na površini  sfere prečnika R koja okružuje izotropnu antenu [3,17].
Takođe, iz ovog izraza se može zaključiti da se gustina snage elektromagnetskog polja smanjuje sa povećanjem rastojanja od izvora zračenja (predajnika), te da je gustina snage obrnuto proporcionalna kvadratu rastojanja od izvora (slika 1.15-a).
Ovo je zakon po kome gustina energije opada sa kvadratom udaljenosti od izvora zračenja. Ovaformula je tačna za predajnik koji zrači u svim pravcima ili za predajnik koji zrači na ograničenom dijelu sfere.

 

Stvarna antena ima usmjerenost u pravcu maksimuma zračenja veću od 1 (ili 0dB), a izračena snaga je zbog gubitaka na antenskoj strukturi manja od snage signala na ulazu (slika 1.15-b).
U tom slučaju, gustina snage elektromagnetskog polja u nekoj udaljenoj tački zavisi  od instalisane snage  predajnika, kao i od pojačanja (G) upotrebljene antene, tako da se  za izračunavanje gustine snage  koristi formula:

gde je:

Sd – snaga gustine u W/m² u osi glavnog snopa (lista) zračenja antene (kodusmjerenih antena), ili u bilo kom  smjeru kod  neusmjerenih antena; G-  pojačanje antene izraženo kao odnos (a ne u decibelima). Tako, napr. pojačanju antene od 8 dBodgovara odnos sna­ge od 6 ,3 puta, i ovaj se broj unosi u datu formulu;
P –  izlazna snaga predajnika u vatima;
R –  rastojanje tačke u kojoj se izračunava gustina sna­ge od predajne antene, u  metrima.

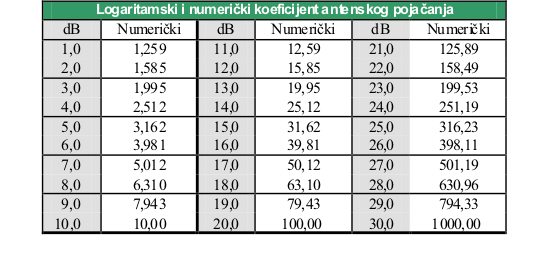
     U tabeli 1.3, dati su logaritamski i numerički koeficijenti antenskog pojačanja za opseg od 1,0 do 30,0 dB.

   

1.3.5.  Izlazna snaga radio frekvencijskog predajnika (top)

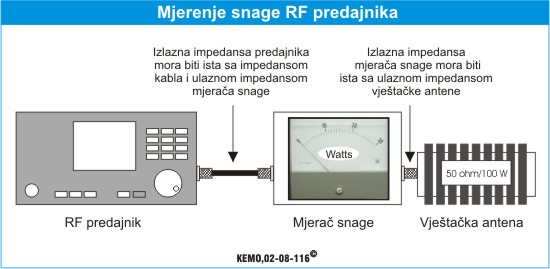
Izlazna snaga RF predajnika (output) uglavnom se  izražava u vatima ( W). To je ustvari stvarna (instalisana) snaga predajnika izmjerena na izlaznom pruključku za antenu koji je zaključen odgovarajućom impedansom u obliku tzv. vještačke antene. Princip mjerenja izlazne snage predajnika prikazan je na slici 1.16.

   

1.3.6.  Efektivna izotropno zračena snaga (top)

Prava izračena snaga u slobodnom prostoru zavisi od pojačanja (G) rezonantne antene na koju je ta jpredajnik priključen, i gubitaka nastalih u antenskom kablu i konektorima (Ploss) narelaciji: predajnik-antena [1,16,17].
Zbog toga je uveden pojam sakojim je definisana jačina izračenog elektromagnetskog polja EIRP (EffectiveIzotropicRadiatedPower) – efektivna izotropno zračena snaga.
Efektivna izotropno zračena snaga (EIRP) je stvarna RF snaga izmjerena u glavnoj osi snopa zračenja ili fokusnoj tački antene.
Ona je jednaka zbiru transmitovane (privedene) snage predajnika u antenu (u dBm) i dBi (pojačanje antene u odnosu na izotropni radijator koji predstavlja ”perfektnu” antenu koja zrači podjednako u svim smjerovima, a  čije je teoretsko pojačanje 0 dB) antenskog pojačanja.

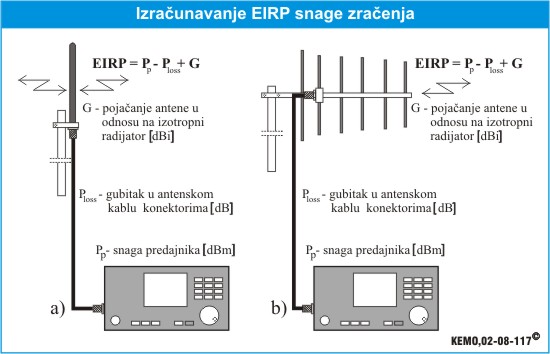
Ako se uzme u obzir gubitak na prenosnom mediju Ploss (slabljenje koje unosi koaksijalni kabal i konektori), dobijamo: gdje je: Pp–   Snaga predajnika [dBm], Ploss– gubitak zbog slabljenja u antenskom kablu i konektorima od predajnika do antene  [dB] i G–     pojačanje antene u odnosu na izotropni radijator [dBi]

 

 

U sličaju primjera 2 (sa antenom pod ”a”), vidimo da se ukupna (instalisana) snaga iz predajnika nije izračila u prostor zbog gubitka u antenskom kablu i konektorima, a sama antena nema pojačanje.
U sličaju primjera 2 (sa antenom pod ”b”), vidimo da je snaga  zračenja (i pored gubitka 2 dB gubitka u antenskom kablu i konektorima) znatno veća u jednom pravcu zbog pojačanja antene od 6 dB u tom pravcu.
Matematički gledano mogli bi doći do pogrešnog zaključka da je antena kao pasivni elemenat povećala snagu predajnika, što bi predstavljalo svojevrsni ”perpetumobile” u radio tehnici. Ustvari, antena je sa svojom konstrukcijom, fokusirala izračenu EM energiju u jednom pravcu, oblikujući kružni dijagram isijavanja (sferni oblik prelazi u elipsoid) i na taj način izračenu elektromagnetsku energiju usmjerila samo u jednom pravcu. Na taj način je povećana gustina snage u osi glavnog snopa zračenja antene iako je snaga predajnika ostala ista.
Ove relacije su jako važne jer predstavljaju primjer koliko pojačanje antene  utiče na gustinu snage zračenja za pravac najvećeg dobitka – pojačanja antene.
Pojednostavljeno, svaka 3 dBi antenskog pojačanja, pojačavaju  snage zračenja za 100%  u  pravcu ose glavnog snopa zračenja.
Dakle, ako imamo EIRP 100 mW na anteni od 9 dBi  samo promjenom antene od 9 dBi na 12 dBi dobijamo snagu zračenja za taj pravac 200 mW, a kao rezultat toga dobićemo proporcionalno veću gustinu snage u nekoj tački koja se nalazi u osi glavnog snopa zračenja antene.
Efektivna izotropno zračena snaga (EIRP), može se prikazati i kao proizvod snage predajnika (Pp) i pojačanja antene (G):

U tom slučaju snaga predajnika se izražava u (W) vatima, dok se antensko pojačanje izražava u numeričkom koeficijentu pojačanja umjesto u logaritamskom (vidi tabelu 1.3). Tako npr. za antenu koja je imala 6 dB logaritamskog pojačanja, numerički koeficijent sa kojim je definisano isto pojačanje iznosi: 3,981.
U praksi se u nekim slučajevima za izračunavanje koristi snaga koju zrači polutalasni dipol i naziva se efektivna zračena snaga ERP (Effective  Radiated Power), koja se može izraziti preko EIRP (Effective Izotropic Radiated Power): 

Vrati se na početak.

Izvod iz prvog poglavlja knjige: ČOVJEK U BLISKOM RADIOFREKVENCIJSKOP POLJU, autora Kemala Dervića.